Условия устойчивости (робастности) управления для систем с пи регуляторами

Системы, способные поддерживать качество управления близкое к оптимальному при изменении тех или иных, влияющих на него факторов, принято называть робастными (устойчивыми). Часто к таким факторам относятся статистические характеристики возмущающих воздействий. Название "робастный" происходит от английского слова robust, имеющего значения: крепкий, сильный, грубый.

Поскольку значение величины , как видно из выражения (4 10), зависит от расположения полюсов замкнутой системы и ограничения (4 11), (4 12) и (4 15) также устанавливают к нему определенные требования, то желательно выяснить при каком расположении полюсов выполняется требование (4 9).

Искомое расположение полюсов устанавливает следующее математическое утверждение:

Теорема 5.1. Максимум свободного члена характеристического полинома замкнутой линейной стационарной системы при ограничениях (4 11), (4 12) и (4 15) достигается тогда и только тогда, когда расположение ее полюсов удовлетворяет следующим требованиям:

(5.1)

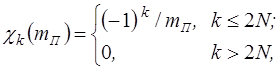
а - целая часть отношения ( - порядок характеристического полинома).

Следовательно, параметры настройки регулятора следует выбирать таким образом, чтобы обеспечить выполнение условий (5.1), т.к. при этом выполняется требование (4 9) и введенные ограничения на расположение полюсов замкнутой системы.

Эти ограничения, в отличие от критерия , иногда называют показателями качества управления, т.к. они также характеризуют степень успешности достижения цели управления, но по отношению к ним не выдвигаются экстремальные требования, аналогичные (4 9).

Для оценки эффективности робастного управления желательно определить границы интервала частот, в котором возможно выполнить условия (4 7), т.к. на практике иногда удается оценить полосу частот, в которой возмущающие воздействия проявляют себя заметным образом.

Добиться выполнения указанных условий можно при расположении полюсов замкнутой системы в соответствии с требованиями (5.1).

Поскольку от расположения полюсов зависит знаменатель АЧХ замкнутых систем, то при выполнении (5.1) он должен максимизироваться в интервале частот , способствуя тем самым выполнению условий (4 7).

Значение величины определяется на основании следующего математического утверждения:

Теорема 5.2. Для замкнутой линейной стационарной системы при ограничениях (4 11), (4 12) и (4 15) максимум величины достигается при любом значении , удовлетворяющем неравенству , если расположение полюсов системы удовлетворяет требованиям (5.1). Причем величина является решением уравнения

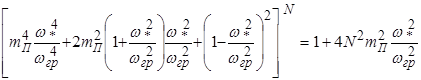, (5.2)

где собственная частота системы определяется выражением

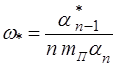, (5.3)

а - целая часть отношения ( - порядок характеристического полинома).

Выполнение требований (4.1) обеспечивает оптимизацию наряду с частотными, также и временных динамических характеристик замкнутой системы, на что указывает следующее математическое утверждение:

Теорема 5.3. Для того чтобы при ограничениях (4 11), (4 12) и (4 15) достигался максимум показателя необходимо и достаточно обеспечить расположение полюсов системы в соответствии с требованиями (5.1).

Лучшие статьи по информатике

Электронные трансформаторы на основе высокочастотных структур с переключаемыми конденсаторами для автономных систем электроснабжения
Из основных тенденций развития радиоэлектронных средств (РЭС) и систем связи следует отметить с одной стороны все возрастающую степень использования интегра ...

Разработка сети передачи данных Нуринского РУТ Карагандинской области на основе создания цифровых РРЛ
Оцифрованные магистрали, на базе которых строятся современные сети передачи информации, должны быть стандарта SDH (Synchronous Digital Hierarchy -это синхро ...

Проектирование канала сбора аналоговых данных микропроцессорной системы
Применяя микропроцессоры и микро-ЭВМ для контроля за сложными производственными процессами, можно обрабатывать в реальном масштабе времени сигналы, поступаю ...