Моделирование системы автоматического управления средствами MATLAB

Исследование цифровой системы на устойчивость

Непрерывная система устойчива, если все корни ее характеристического уравнения лежат в левой полуплоскости. При исследовании дискретных систем вместо р используется новая переменная z =.Преобразование z =отображает левую полуплоскость плоскости р в область, ограниченную окружностью единичного радиуса на плоскости z, при этом мнимая ось отражается в саму эту окружность [1]. Следовательно, для того чтобы системы была устойчива необходимо и достаточно, чтобы корни характеристического уравнения лежали внутри единичной окружности.

Как видно из рис. 3.2.11, все корни характеристического уравнения лежат внутри единичной окружности, следовательно, проектируемая цифровая система устойчива.

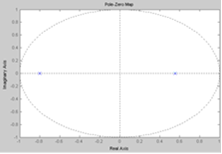
Рис. 3.2.11. Проверка устойчивости ЦСАУ

Лучшие статьи по информатике

Применение цифровых фотокамер для осуществления регулярной видеосъемки в образовательных учреждениях
цифровая фотокамера видеосъёмка Современная жизнь диктует новые требования к качеству изобразительного контента. Если в 1980-90 е года черно-белая картинка с ...

Технология создания первичной фонограммы в условиях записи чистового звука к видеофильму формата DVCAM с использованием PC для записи звука на съемочной площадке
Главные цели, поставленные автором для данной курсовой работы - показать работу звукорежиссера в условиях съемки видеофильма формата DVCAM с использованием п ...

Построение и анализ математической модели объекта управления
Построим математическую модель объекта управления в пространстве состояния Рисунок 2 Структурная схема ОУ В схеме четыре элемента, запасающих э ...