Частота сообщения

Задание 1

Рассчитать и построить амплитудно-частотный спектр ЧМП сигнала и определить полосу частот, если частота модулирующего сообщения , частота несущей , амплитуда несущей , индекс модуляции .частотный бергер хэмминг код

Решение:

Выражение для ЧМП сигнала:

(1.1)

где - модулирующий сигнал в виде последовательности прямоугольных импульсов, , -девиация частоты т.е величина максимального отклонения от несущей Согласно [1] выражение для расчета составляющих спектра ЧМП сигнала:

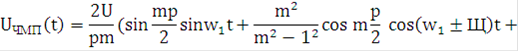
Практическая ширина спектра ЧМП сигнала:

Подставим численные значение в (1.3):

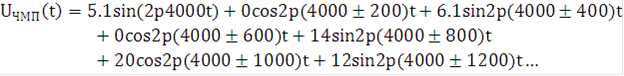
Расчет амплитуд и частотных составляющих ЧМП сигнала сведем в таблицу.

Значения амплитуд и частот гармонических составляющих ЧМП сигнала

Составляющие на частотах	Амплитуда, В	Частота, Гц
	5.1	4000
	0	4200
	0	3800
	6.1	4400
	6.1	3600
	0	4600
	0	3400
	14	4800
	14	3200
	20	5000
	20	3000
	12	5200
	12	2800

Спектр ЧМП сигнала в соответствии с таблицей 1.1 имеет вид:

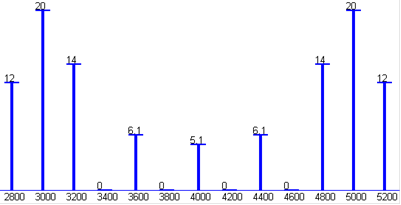
Рисунок 1.1 - Амплитудно-частотный спектр ЧМП сигнала

Мощность ЧМП сигнала на единичном сопротивлении:

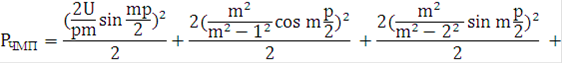
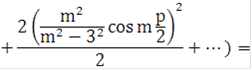
Вывод.

Спектр ЧМП сигнала содержит 13 составляющих на частотах, приведенных в таблице, занимает полосу частот равную 6000 Гц, суммарная мощность всех составляющих равна 790Вт.

Задание 2

Рассчитать и построить амплитудно-частотный спектр ЧМ сигнала и определить полосу частот, если частота модулирующего сообщения , амплитуда модулирующего сообщения частота несущей , амплитуда несущей .

Решение:

Модулирующий сигнал описывается выражением:

Поднесущая:

Выражение для ЧМ сигнала:

,

где -индекс модуляции.

Выражение для расчета спектра ЧМ сигнала:

-

Практическая ширина спектра ЧМ сигнала:

ДF=2000Гц

Значения Бесселевых функций для m = 5

0,18	0,33	0,05	0,36	0,39	0,26	0,13	0,05

Расчет амплитуд и частотных составляющих ЧМ сигнала сведем в таблицу.

Значения амплитуд и частот гармонических составляющих ЧМ сигнала

Составляющие на частотах	Амплитуда, В	Частота, Гц
	7.2	4000
	13.2	3800
	13.2	4200
	2	3600
	2	4400
	14.4	3400
	14.4	4600
	15.6	3200
	15.6	4800
	10.4	3000
	10.4	5000
	5.2	2800
	5.2	5200

Спектр ЧМ сигнала в соответствии с таблицей 1.2 имеет вид:

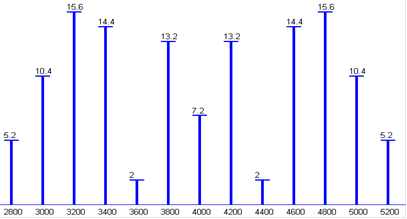
Амплитудно-частотный спектр ЧМ сигнала

Мощность ЧМ сигнала на единичном сопротивлении:

=

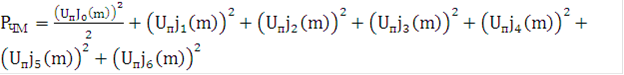Вывод.

Спектр ЧМ сигнала занимает полосу частот равную 2000 Гц, на которой находятся 11 составляющих, суммарная мощность всех составляющих равна 790Вт.

Задание 3

Рассчитать и построить амплитудно-частотный спектр АМ-АМ сигнала и определить полосу частот, если амплитуда модулирующего сигнала амплитуда поднесущей , частота несущей , частота поднесущей , частота модулирующего сигнала , коэффициент глубины модуляции на первой ступени , на второй .

Решение:

Модулирующее сообщение описывается выражением

Поднесущая

Несущая

Амплитудно-модулированный сигнал может быть представлен в виде:

Подставив из (1.11) -(1.12) Uc(t) и w1 в (1.14) получим:

Тогда АМ-АМ сигнал принимает вид:

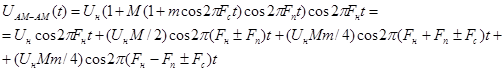
Амплитуда несущей:

где k=1 коэффициент пропорциональности.

Полоса частот, занимаемая АМ-АМ:

Подставим числовые значения в:

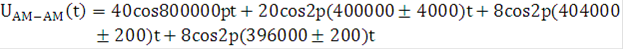
Расчет амплитуд и частотных составляющих АМ-АМ сигнала сведем в таблицу.

Значения амплитуд и частот гармонических составляющих АМ-АМ сигнала

Составляющие на частотахАмплитуда, ВЧастота, Гц
40400000
20404000
20396000
8404200
8403800
8396200
8395800

Спектр АМ-АМ сигнала в соответствии с таблицей 1.3 имеет вид:

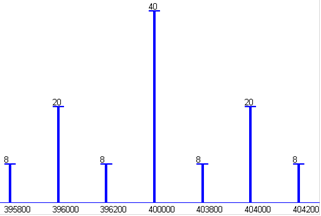
Рисунок 1.3 - Амплитудно-частотный спектр АМ-АМ сигнала

Мощность АМ-АМ сигнала на единичном сопротивлении:

Вывод.

Спектр АМ-АМ сигнала содержит 7 составляющих на частотах, приведенных в таблице, занимает полосу частот равную 8400 Гц, суммарная мощность всех составляющих равна 1328Вт.

Задание 4

Закодировать число 120 в коде Бергера и сделать вывод о корректирующих свойствах.

Решение.

Число информационных символов:

Число 120 в двоичном коде имеет вид 1111000. Контрольные символы в этом коде представляют разряды двоичного числа в прямом или инверсном виде количества единиц или нулей, содержащихся в исходной кодовой комбинации.

Определим число контрольных символов:

=3,

Для комбинации F(x)= 1111000 запишем количество единиц в двоичном коде в прямом виде: 100 - контрольные символы, тогда закодированная комбинация будет иметь вид F'(x)= 1111000 100.

Пусть кодовая комбинация F(x) была искажена помехами и поступила в виде F'(x)= 1111010 100, где искаженные символы подчеркнуты, тогда 101100=001 искажение обнаружено.

Вывод

. Данный код обнаруживает все одиночные и большую часть многократных ошибок.

Задание 5

Закодировать число 1111000 кодом Хэмминга с d = 4 и сделать вывод о корректирующих свойствах.

Решение.

Определим число контрольных символов. Для кода Хэмминга с d=3:

k=7

r=4

Тогда для кода Хэмминга с d=4:

r=4+1=5

Состав передаваемой кодовой комбинации:

F(x)=

Определим состав контрольных символов. Для этого составляют колонку ряда натуральных чисел в двоичном коде, число строк в которой равно n, а рядом справа, сверху вниз проставляются символы комбинации кода Хемминга, записанные в следующей последовательности:

- 0111 -

- 1000 -

- 1001 -

- 1010 -

- 1011 -

-

Тогда контрольные символы определяются по следующим образом:

r1=k7k6k4k3k1=11100=1=k7k5k4k2k1=11100=13=k6k5k4=111=1

r4=k3k2k1=000=0

r5=11111110000=1

В итоге на выходе будет комбинация F(X) =111111100001

Пусть кодовая комбинация F(x) была искажена помехами и поступила в виде F'(x)=110111100001, где искаженные символы подчеркнуты, где искаженные символы подчеркнуты.

В результате декодирования:

S1=r1k7k6k4k3k1=101100=1

S2=r2k7k5k4k2k1=101100=1=r3k6k5k4=1111=04=r4k3k2k1=0000=0

110111100001=1

Синдром и , что указывает на то, что искажен третий разряд кодовой комбинации .

Вывод.

Код Хэмминга с d=4 может обнаруживать двойные ошибки и исправлять одиночные.

Задание 6

Закодировать число 120 (11110000) кодом Файра с bs = 4 и bm = 5 сделать вывод о корректирующих свойствах.

Решение.

Образующий многочлен кода Файра определяется из выражения

где - неприводимый многочлен степени 4, принимаем t=4

Из соответствующих таблиц выбираем неприводимый многочлен P(X)= = 10011.

4+5-18,

принимаем С=8

Находим . Видим, что C на E нацело не делится. Число контрольных символов . Длинна кода равна

n=НОК=НОК(15,8) = 120

В итоге получаем циклический код (120, 108). Образующий многочлен Файра равен

=()()== = 1001100010011

Далее кодирование осуществляется так же как при циклическом коде с d=3.

Так как необходимо закодировать только одно сообщение , а не весь ансамбль двоичных кодов с , то в дальнейшем будем придерживаться процедуры кодирования, выполняемой по уравнению

Выбираем одночлен . Тогда

11110000 000000000000

Разделим полученное выражение на

находим остаток 100100000110

Следовательно, передаваемая закодированная комбинация будет иметь вид

F(X) = 11110000 100100000110

Пусть кодовая комбинация F(x) была искажена помехами и поступила в виде F'(x)= 11101111 100100000110, где искаженные символы подчеркнуты. Разделим F'(x) на образующий полином:

получили остаток 011011110111, следовательно, в полученной комбинации есть ошибка.

Вывод.

Код Файра с ds = 4 и dm = 5 может обнаруживать пакеты ошибок длиной равной 5.

Лучшие статьи по информатике

Принципиальная схема усилителя на основе полевых и биполярных транзисторов
Аналоговыми называются устройства, у которых сигналы являются непрерывными функциями времени. К основным классам аналоговых устройств относятся: усилители, ...

Расчет антенны для земной станции спутниковой системы связи (ЗССС)
Зеркальные антенны являются наиболее распространёнными остронаправленными антеннами. Их широкое применение в самых разнообразных радиосист ...

Разработка сети передачи данных Нуринского РУТ Карагандинской области на основе создания цифровых РРЛ
Оцифрованные магистрали, на базе которых строятся современные сети передачи информации, должны быть стандарта SDH (Synchronous Digital Hierarchy -это синхро ...